Demonstration: Blind Speech Enhancement
Anechoic speech signals sampled at 16 kHz are taken from the TIMIT corpus [1]. For Experiment 1, the room impulses responses from the source to a 32-channel spherical microphone array are simulated using the SMIRgen tool in [2]. For Experiment 2, the acoustic impulse response and babble noise signals are taken from the 32-channel Eigenmike [3] recordings in the ACE corpus [4].
The noisy and reverberant speech at each microphone is generated by convolving the anechoic speech with the room impulse response before adding noise at the desired SNR. Eigenbeam signals are generated using the spherical harmonic (SH) transform [5,6]. The sequential matrix diagonalisation (SMD) algorithm [7] is used for all PEVD processing.
The algorithms used in the comparison include
- Eigenbeam χ_0^0(n) [5,6]
- KLT{Eigenbeam χ_0^0} by applying the KLT in [8] to the χ_0^0(n) eigenbeam
- Eigenbeam χ_1^1(n) [5,6] is directed at the source in Experiment 1
- PEVD L1 [9] using 4 eigenbeam signals generated from the first-order approximation of the sound field in the SH domain (Proposed)
- PEVD L2 [9] using 9 eigenbeam signals generated from the second-order approximation of the sound field in the SH domain (Proposed)
- RAW PEVD [10] which uses the SMD algorithm [7] to directly process the 32-channel raw microphone signals
Audio Examples
The audio player is built using the trackswitch.js tool in [12].
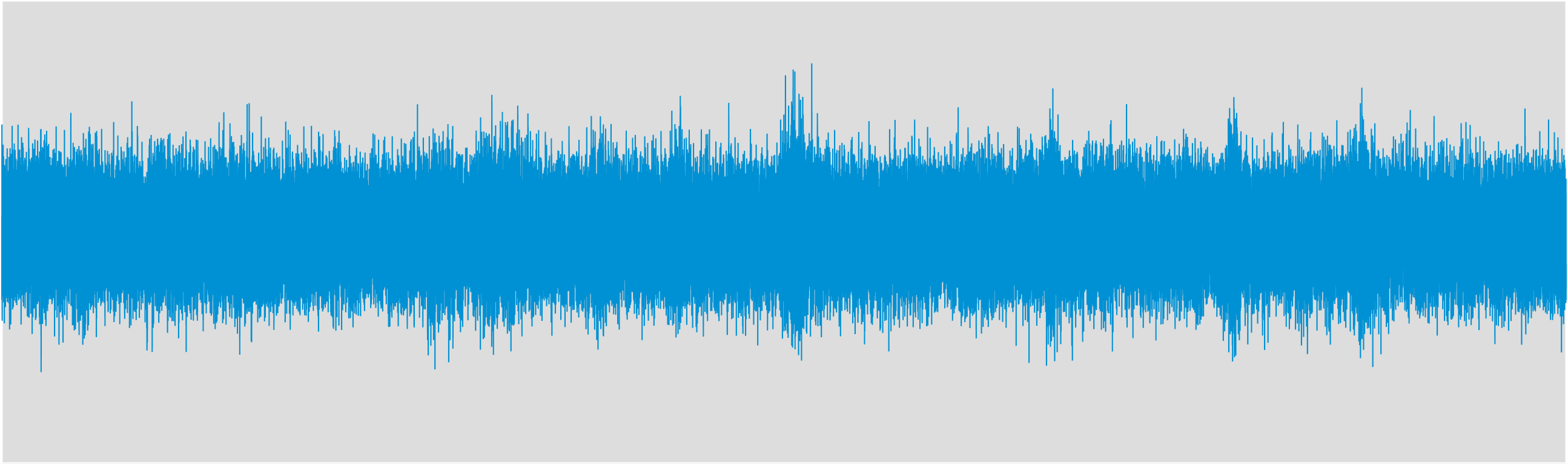
Speech in SMIRgen simulated room, corrupted by -10 dB white noise.
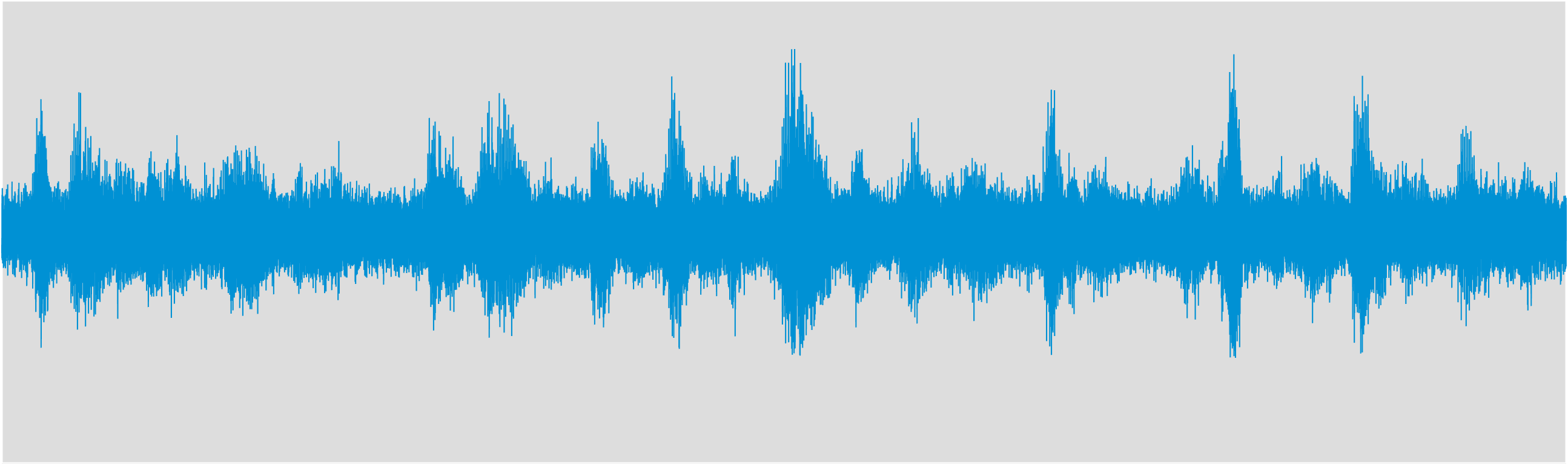
Speech in SMIRgen simulated room, corrupted by 0 dB white noise.
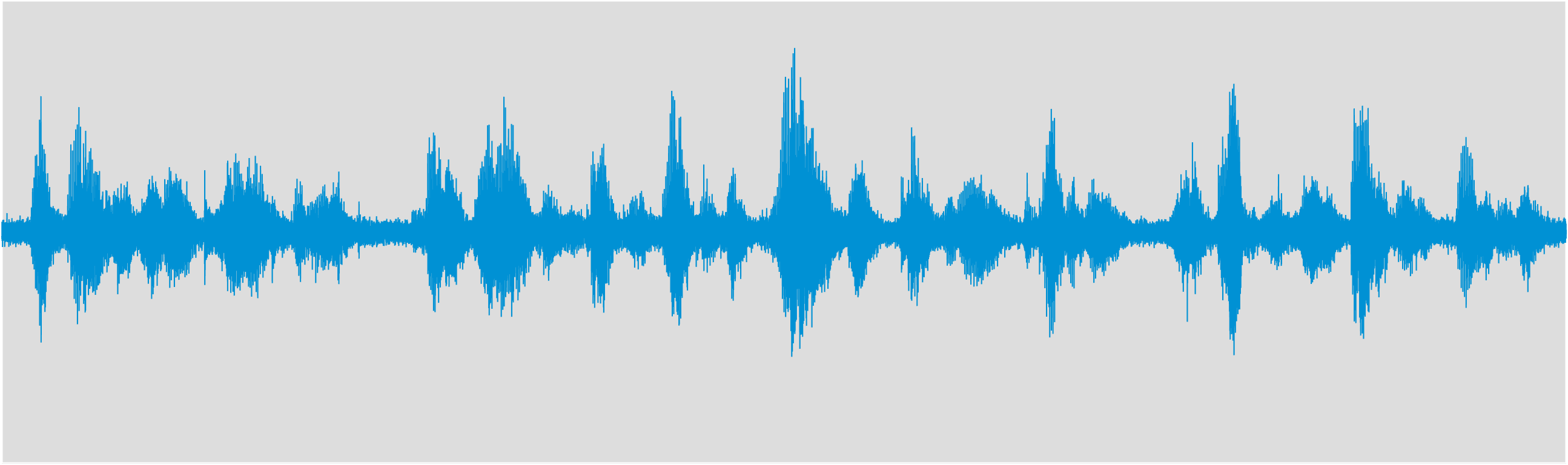
Speech in SMIRgen simulated room, corrupted by 10 dB white noise.
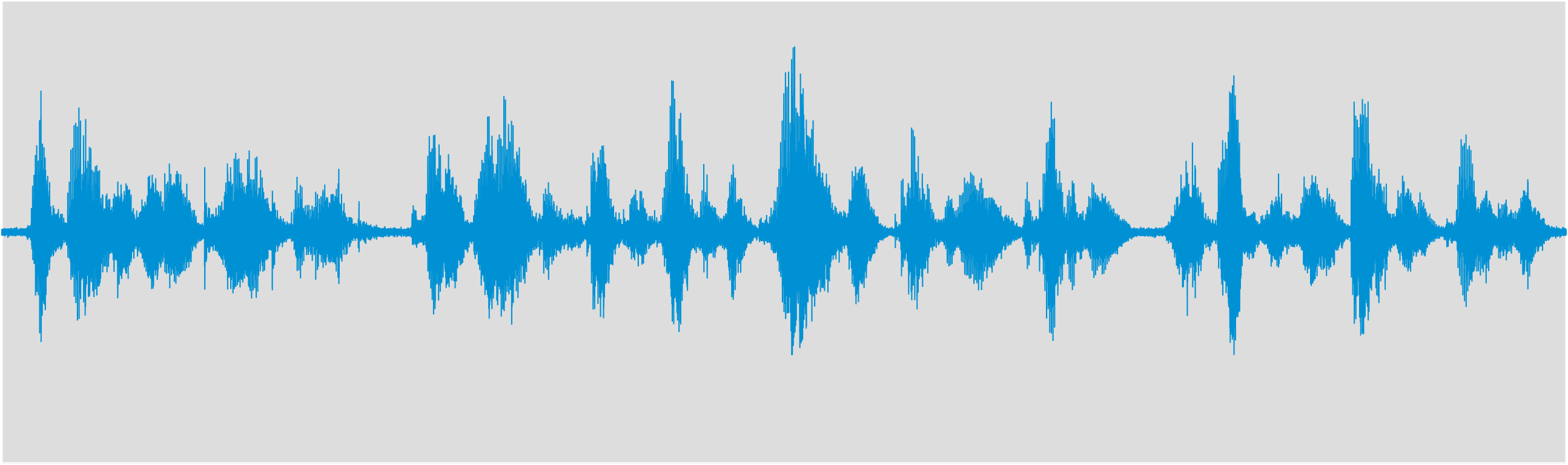
Speech in SMIRgen simulated room, corrupted by 20 dB white noise.
Speech in ACE Lecture Room 2, corrupted by -10 dB babble noise.
Speech in ACE Lecture Room 2, corrupted by 0 dB babble noise.
Speech in ACE Lecture Room 2, corrupted by 10 dB babble noise.
Speech in ACE Lecture Room 2, corrupted by 20 dB babble noise.
References
[1] J. S. Garofolo, L. F. Lamel, W. M. Fisher, J. G. Fiscus, D. S. Pallet, N. L. Dahlgren, and V. Zue, "TIMIT acoustic-phonetic continuous speech corpus," Linguistic Data Consortium (LDC), Philadelphia, Corpus, 1993.
[2] D. P. Jarrett, E. A. P. Habets, M. R. P. Thomas and P. A. Naylor, “Rigid sphere room impulse response simulation: Algorithm and applications,” J. Acoust. Soc. Am., vol. 132, no. 3, pp. 1462-1472, Sep. 2012.
[3] “EM32 Eigenmike microphone array release notes (v 17.0),” M. H. Acoust., NJ USA, Hardware, Oct. 2013. [Online]. Available: https://www.mhacoustics.com/sites/default/files/ReleaseNotes.pdf
[4] J. Eaton, N. D. Gaubitch, A. H. Moore, and P. A. Naylor, “Estimation of room acoustic parameters: The ACE challenge,” IEEE/ACM Trans. Audio, Speech, Lang. Process., vol. 24, no. 10, pp. 1681-1693, Oct. 2016.
[5] B. Rafaely, Fundamentals of Spherical Array Processing, Springer Topics in Signal Processing. Springer-Verlag, 2015.
[6] D. P. Jarrett, E. A. P. Habets, and P. A. Naylor, Theory and Applications of Spherical Microphone Array Processing, Springer Topics in Signal Processing. Springer-Verlag, 2017.
[7] S. Redif, S. Weiss, and J. G. McWhirter, “Sequential matrix diagonalisation algorithms for polynomial EVD of para-Hermitian matrices,” IEEE Trans. Signal Process., vol. 63, no. 1, pp. 81-89, Jan. 2015.
[8] Y. Ephraim and H. L. Van Trees, “A signal subspace approach for speech enhancement,” IEEE Trans. Speech Audio Process., vol. 3, no. 4, pp. 251-266, Jul. 1995.
[9] V. W. Neo, C. Evers, and P. A. Naylor, “Polynomial matrix eigenvalue decomposition of spherical harmonics for speech enhancement,” in Proc. IEEE Int. Conf. on Acoust., Speech and Signal Process. (ICASSP), 2021.
[10] V. W. Neo, C. Evers, and P. A. Naylor, “Enhancement of noisy reverberant speech using polynomial matrix eigenvalue decomposition,” IEEE/ACM Trans. Audio, Speech, Lang. Process., vol. 29, pp. 3255-3266, Oct. 2021.
Listening examples audio tool
[11] N. Werner, S. Balke, F.-R. Stöter, M. Müller, B. Edler, "trackswitch.js: A Versatile Web-Based Audio Player for Presenting Scientific Results." 3rd web audio conference, London, UK. 2017. [Online]. Available: https://github.com/audiolabs/trackswitch.js
Related Works on PEVD Algorithms
[12] J. G. McWhirter, P. D. Baxter, T. Cooper, S. Redif, and J. Foster, “An EVD algorithm for para-Hermitian polynomial matrices,” IEEE Trans. Signal Process., vol. 55, no. 5, pp. 2158–2169, May 2007.
[13] V. W. Neo and P. A. Naylor, “Second order sequential best rotation algorithm with Householder transformation for polynomial matrix eigenvalue decomposition,” in Proc. IEEE Int. Conf. on Acoust., Speech and Signal Process. (ICASSP), 2019.
[14] S. Redif, S. Weiss, and J. G. McWhirter, “An approximate polynomial matrix eigenvalue decomposition algorithm for para-Hermitian matrices,” in Proc. Intl. Symp. on Signal Process. and Inform. Technology (ISSPIT), 2011, pp. 421–425.