Fixed Beamformer Design Using Polynomial EVD
This website will demonstrate the design of fixed beamformers using Polynomial EVD developed by Vincent W. Neo, Emilie d'Olne, Alastair H. Moore and Patrick A. Naylor from the Speech and Audio Processing Lab at Imperial College London.
About This Work
Spatially and temporally white and pink noise from the Noisex database [1] are used to train the PEVD filterbanks. The filterbanks for the 4-channel hearing aid array are trained in far-field anechoic environment. For testing ,the sources are clean speech signals from the TIMIT corpus [2]. Testing in reverberant environment uses room impulses responses (RIR) generated using [3]. In both training and testing, 30 dB sensor noise is added to all microphones. The sequential matrix diagonalisation (SMD) algorithm [4] is used for all PEVD processing.
Demonstration
The beamformers used in the comparison include
- Minimum Variance Distortionless Response (MVDR) [5]
- Linearly Constrained Minimum Variance (LCMV) [6]
- Polynomial Eigenvalue Decomposition (PEVD)
Audio Examples
The audio player is built using the trackswitch.js tool in [7].

Two male speakers located at φ1=45 and φ2=50 degrees azimuth in an anechoic environment.
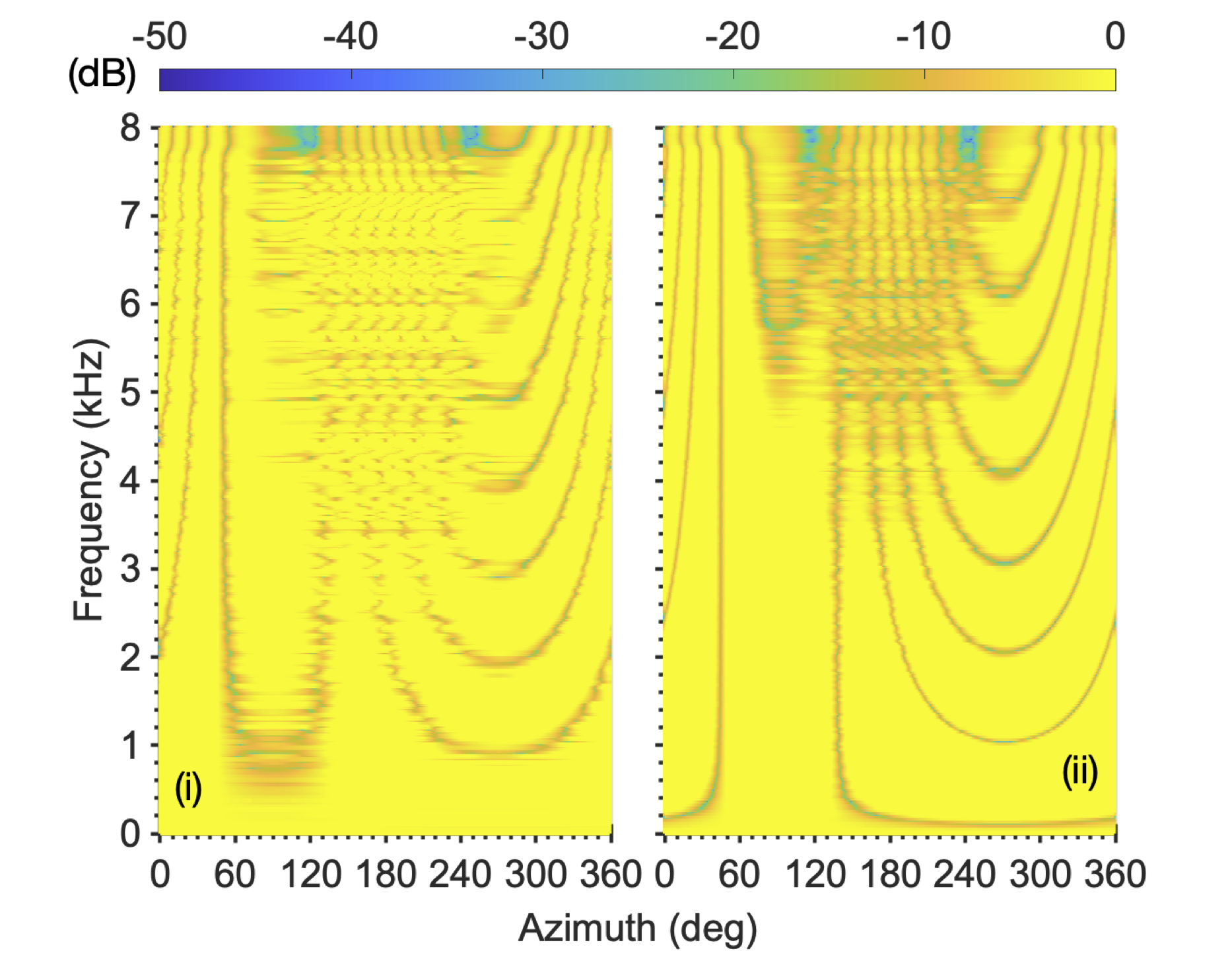
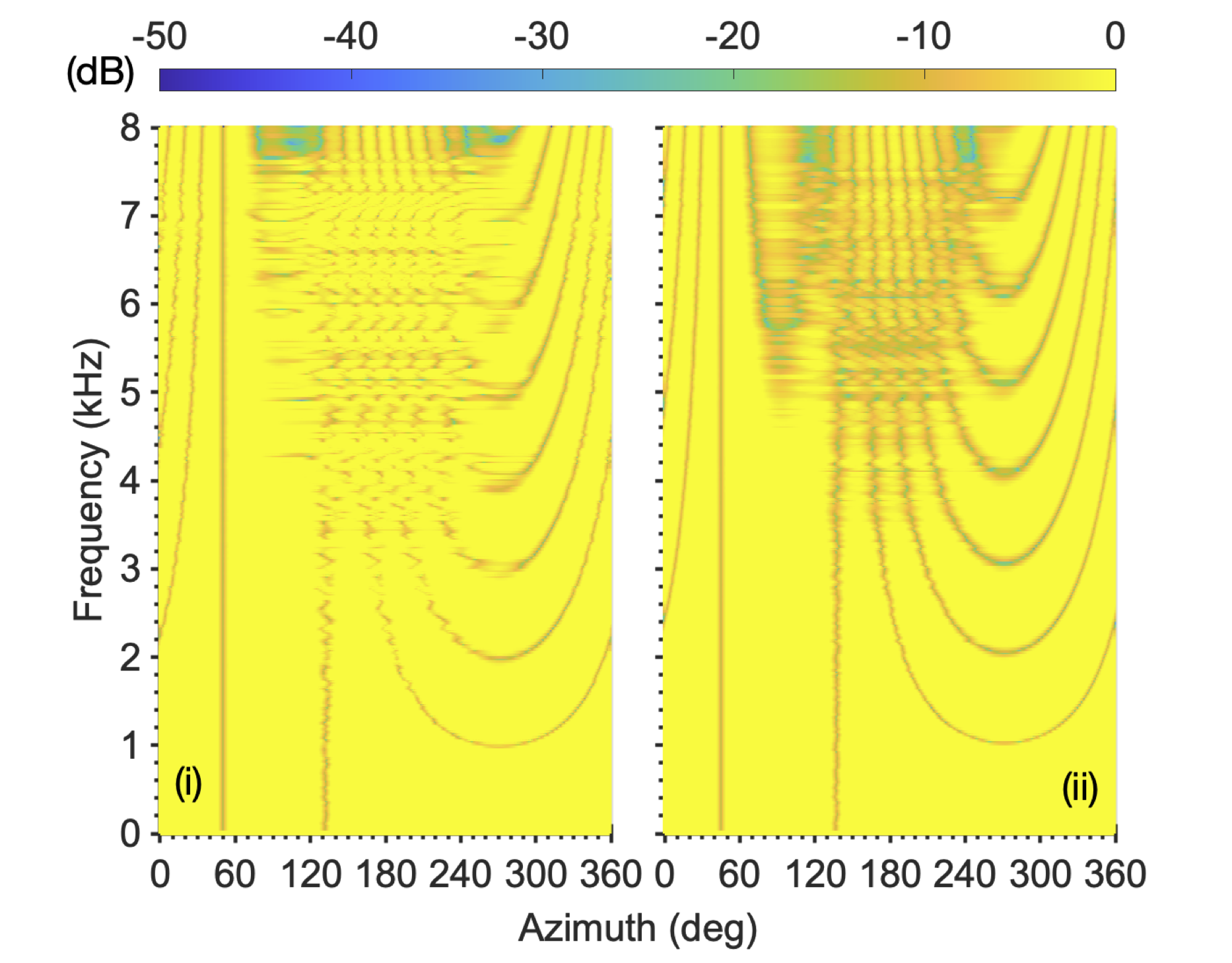
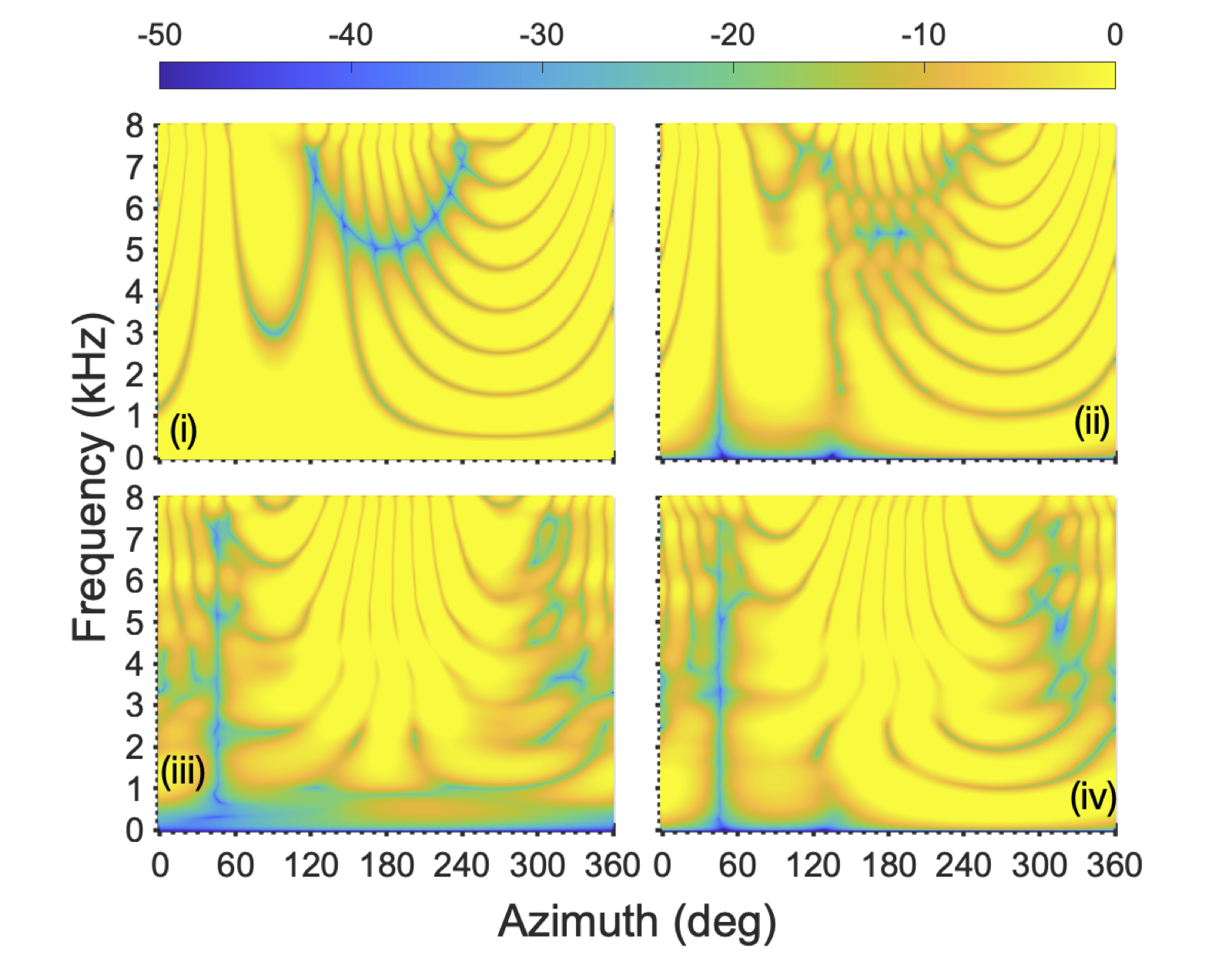
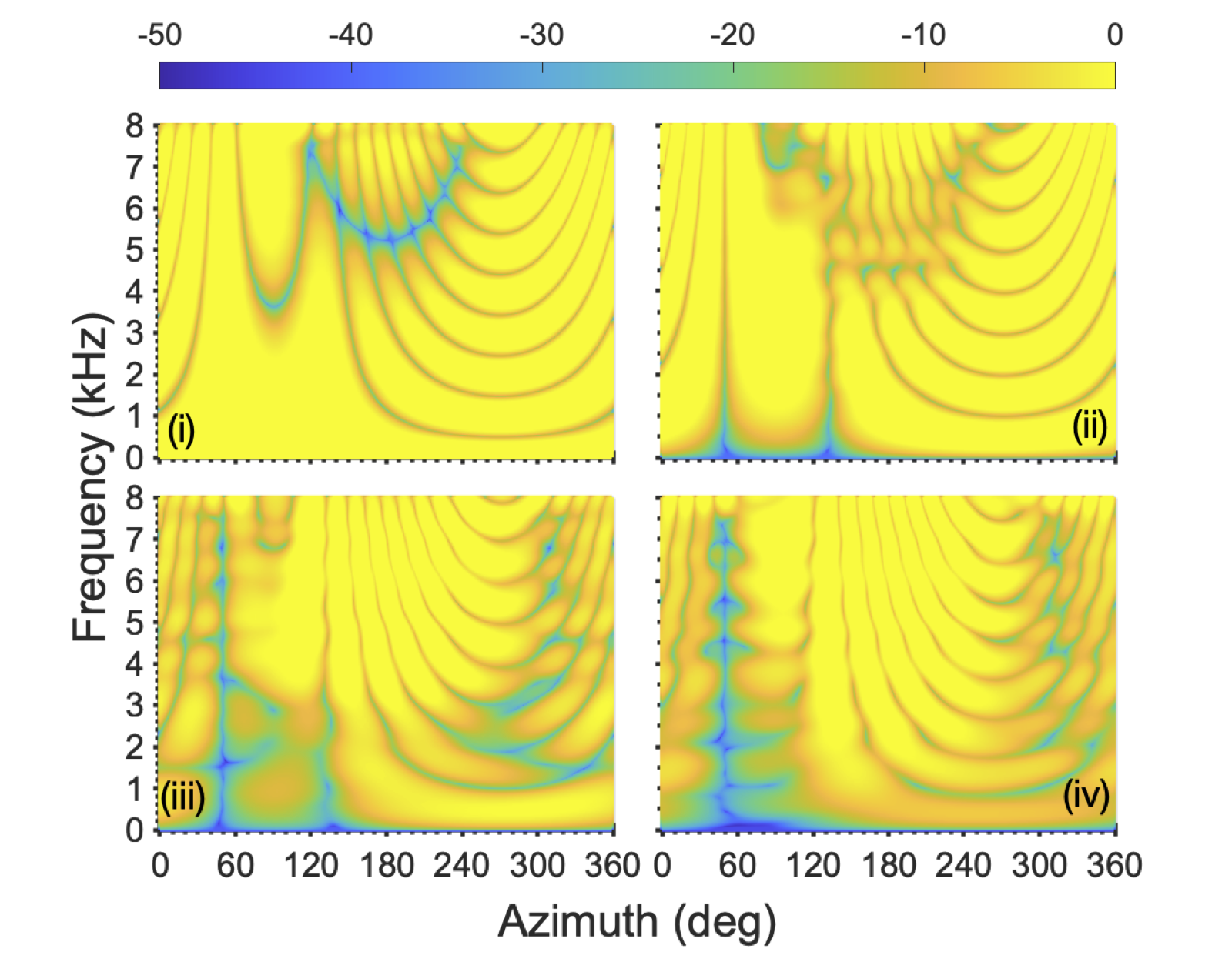

Two male speakers located at φ1=45 and φ2=50 degrees azimuth in a reverberant room.

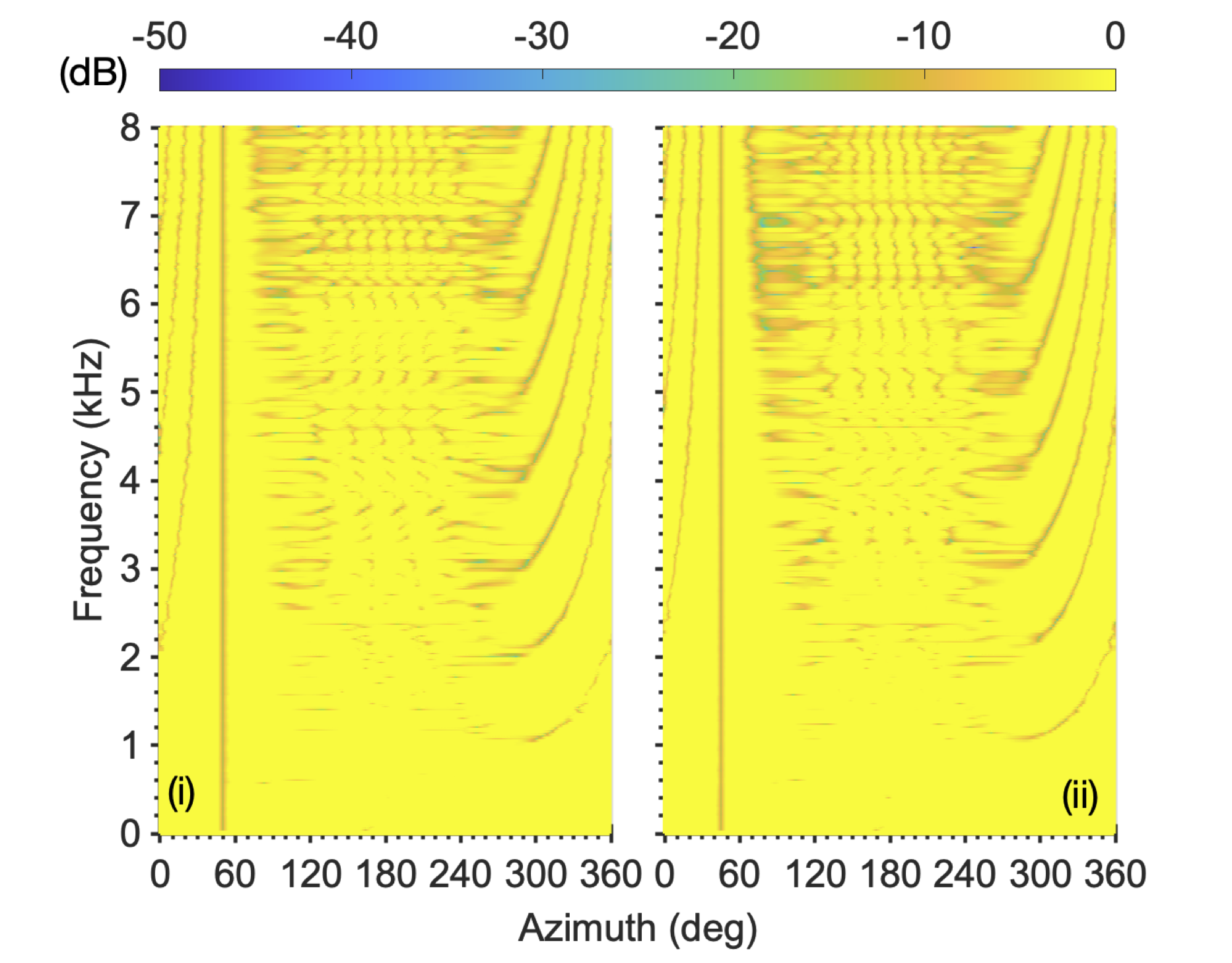



Two male speakers located at φ1=45 and φ2=50 degrees azimuth in an anechoic environment. The second source signal is varied {White/Pink} (W/P).


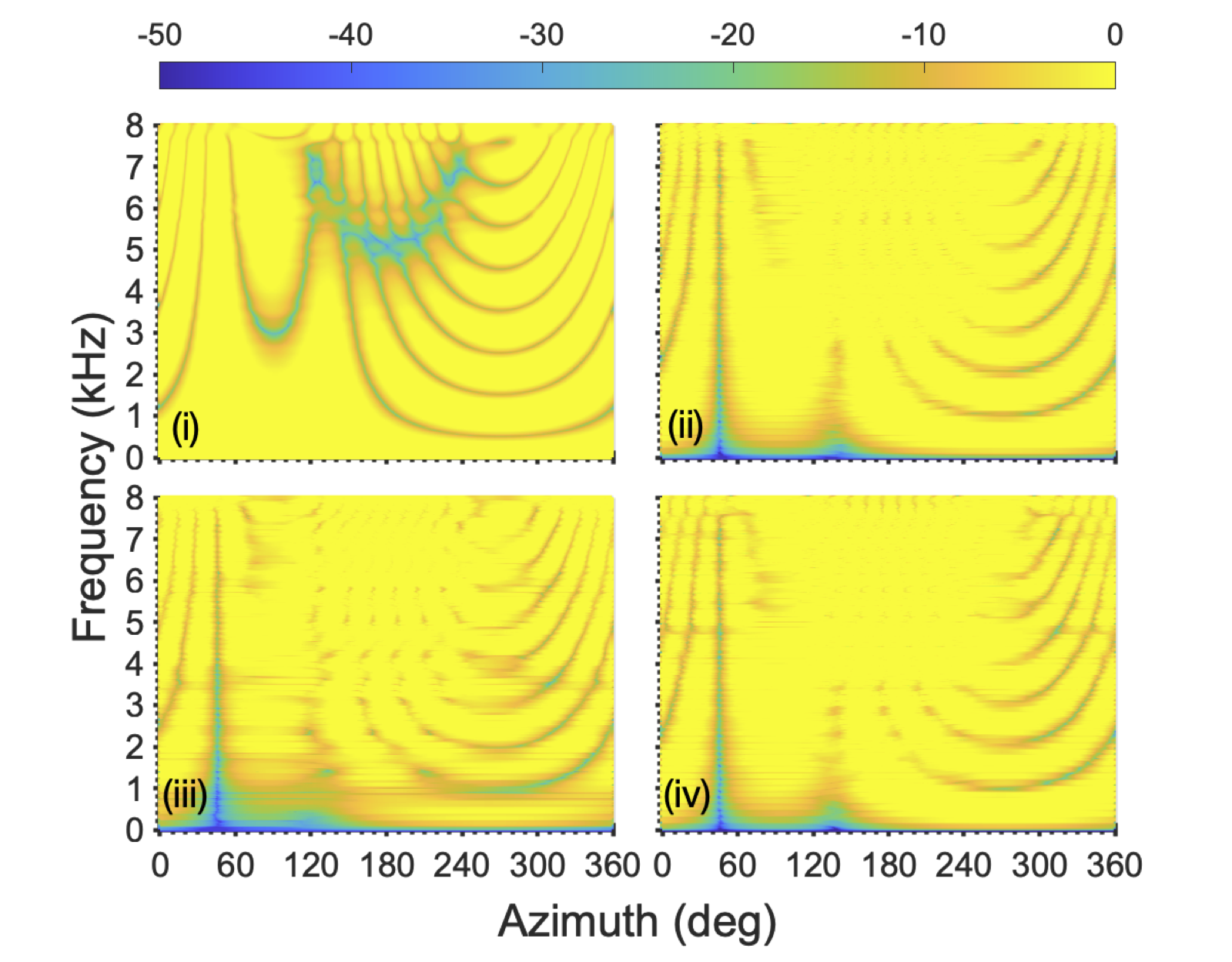
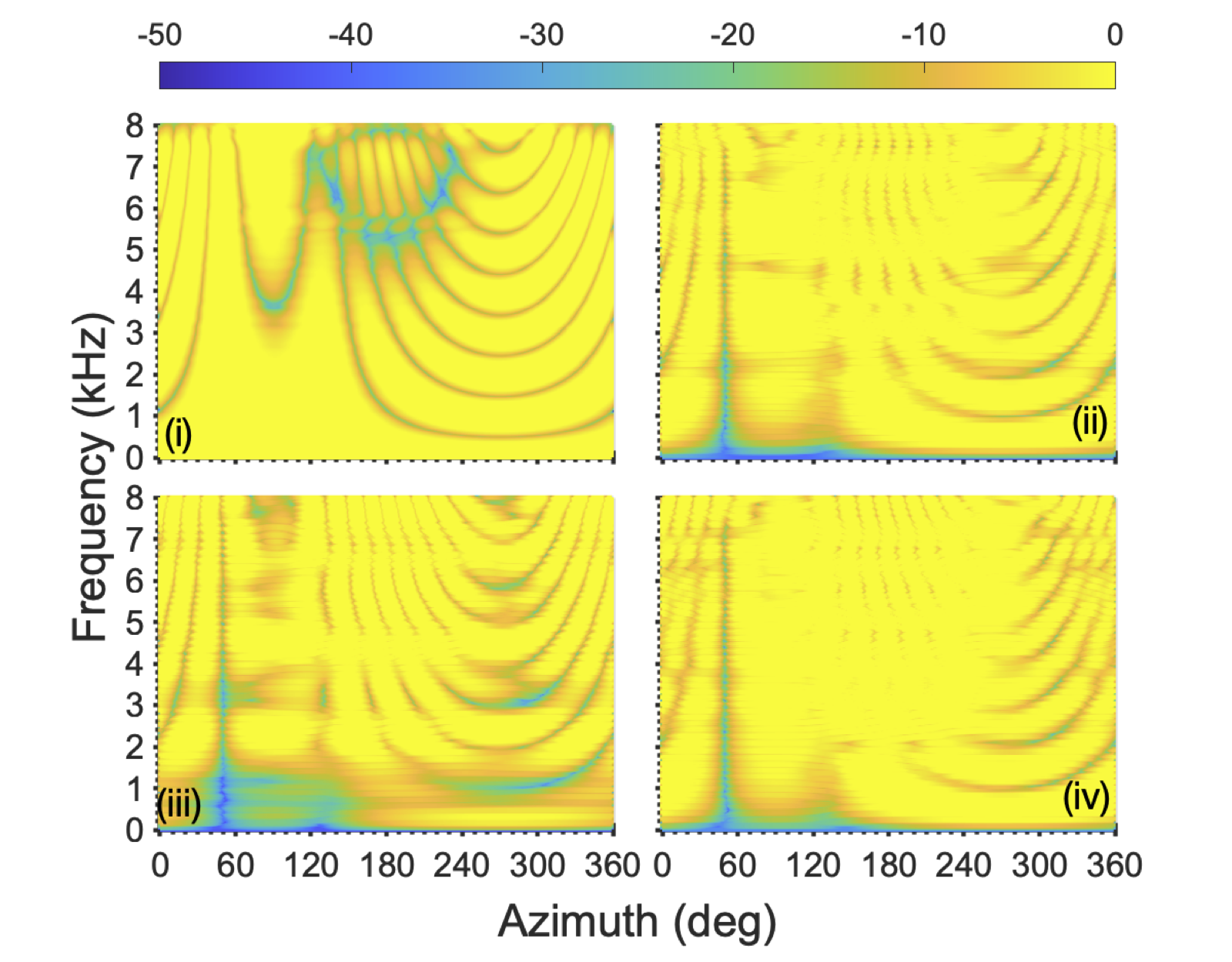
References
[1] A. Varga and H. J. M. Steeneken, “Assessment for automatic speech recognition II: NOISEX-92: A database and experiment to study the effect of additive noise on speech recognition systems,” Apeech Commun., vol. 3, no. 3, pp. 247-251, Jul. 1993.
[2] J. S. Garofolo, L. F. Lamel, W. M. Fisher, J. G. Fiscus, D. S. Pallet, N. L. Dahlgren, and V. Zue, "TIMIT acoustic-phonetic continuous speech corpus," Linguistic Data Consortium (LDC), Philadelphia, Corpus, 1993.
[3] E. A. P. Habets, “Room impulse response generator,” Tecnische Unisersiteit Eindhoven (Tu/e), Tech. Rep., 2006.
[4] S. Redif, S. Weiss, and J. G. McWhirter, “Sequential matrix diagonalisation algorithms for polynomial EVD of para-Hermitian matrices,” IEEE Trans. Signal Process., vol. 63, no. 1, pp. 81-89, Jan. 2015.
[5] M. S. Brandstein and D. B. Ward, Eds., Microphone Arrays: Signal Processing Techniques and Applications. Berlin, Germany: SPringer-Verlag, 2001.
[6] H. L. Van Trees, Optimal Array Processing. Part IV of Detection, Estimation, and Modulation Theory, John Wiley & Sons,2002.
[7] N. Werner, S. Balke, F.-R. Stöter, M. Müller, B. Edler, "trackswitch.js: A Versatile Web-Based Audio Player for Presenting Scientific Results." 3rd web audio conference, London, UK. 2017. [Online]. Available: https://github.com/audiolabs/trackswitch.js
Related Works on PEVD Algorithms
[8] J. G. McWhirter, P. D. Baxter, T. Cooper, S. Redif, and J. Foster, “An EVD algorithm for para-Hermitian polynomial matrices,” IEEE Trans. Signal Process., vol. 55, no. 5, pp. 2158–2169, May 2007.
[9] V. W. Neo and P. A. Naylor, “Second order sequential best rotation algorithm with Householder transformation for polynomial matrix eigenvalue decomposition,” in Proc. IEEE Int. Conf. on Acoust., Speech and Signal Process. (ICASSP), 2019.
[10] S. Redif, S. Weiss, and J. G. McWhirter, “An approximate polynomial matrix eigenvalue decomposition algorithm for para-Hermitian matrices,” in Proc. Intl. Symp. on Signal Process. and Inform. Technology (ISSPIT), 2011, pp. 421–425.